Next: Correntes superficiais Up: Magnetismo da matéria Previous: Equações constitutivas

Interpretação de $\vec{M}$

Sabemos que o momento de dipolo magnético de uma distribuição de correntes estacionárias é

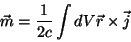$\begin{displaymath} \vec{m}=\frac{1}{2c}\int dV \vec{r}\times \vec{j} \end{displaymath}$

(16)

Qual é o momento de dipolo magnético gerado pelas correntes microscópicas? Usando a expressão (4),

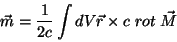$\begin{displaymath} \vec{m}=\frac{1}{2c}\int dV \vec{r}\times c\;rot\;\vec{M} \end{displaymath}$

(17)

Um cálculo simples (veja o Apêndice) leva ao seguinte resultado:

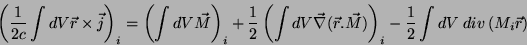$\begin{displaymath} \left(\frac{1}{2c}\int dV\vec{r}\times \vec{j}\right)_i= \le... ...ec{M})\right)_i-\frac{1}{2}\int dV\;div\left(M_i\vec{r}\right) \end{displaymath}$

(18)

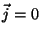Como $\vec{j}=0$ fora do condutor, essas integrais podem ser tomadas como integrais em todo o espaço. A última delas é

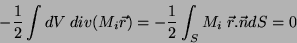$\begin{displaymath} -\frac{1}{2}\int dV\;div(M_i\vec{r})=-\frac{1}{2}\int_SM_i\;\vec{r}.\vec{n}dS =0 \end{displaymath}$

(19)

pois, na segunda integral, a superfície está fora do condutor, onde 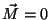$\vec{M}=0$ . Para calcular a penúltima usaremos uma conseqüência do teorema do divergente que eu chamo de teorema de Pauli-Gauss: seja

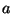uma função (campo escalar). Então, (Apêndice!)

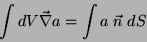$\begin{displaymath} \int dV \vec{\nabla}a=\int a\;\vec{n}\;dS \end{displaymath}$

(20)

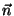onde $\vec{n}$ é, como de costume, a normal externa à superfície

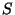que envolve o volume

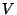. Temos então que

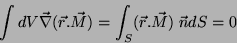$\begin{displaymath} \int dV\vec{\nabla}(\vec{r}.\vec{M})=\int_S(\vec{r}.\vec{M})\;\vec{n}dS=0 \end{displaymath}$

(21)

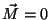pois $\vec{M}=0$ fora do condutor. Em conseqüência,

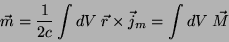$\begin{displaymath} \vec{m}=\frac{1}{2c}\int dV\;\vec{r}\times \vec{j}_m=\int dV \; \vec{M} \end{displaymath}$

(22)

ou seja, 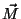$\vec{M}$ é o momento magnético de dipolo por unidade de volume. 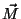$\vec{M}$ é denominado magnetização do material ².

Next: Correntes superficiais Up: Magnetismo da matéria Previous: Equações constitutivas

Henrique Fleming 2002-12-24