Next: Tratamento completo da magnetização Up: Magnetismo da matéria Previous: Interpretação de

Correntes superficiais

Na realidade, um papel essencial é desempenhado pelas correntes superficiais, que foram abandonadas no nosso primeiro tratamento. As correntes de superfície são descritas por um vetor 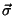$\vec{\sigma}$ definido assim: 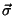$\vec{\sigma}$ é tangente à superfície do condutor; seja

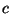uma curva que é a intersecção, com a superfície do condutor, de um plano que o atravessa. Seja 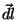$\vec{dl}$ um vetor infinitesimal tangente a essa curva. Então, a corrente superficial é dada por

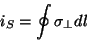$\begin{displaymath} i_S=\oint \sigma_{\perp} dl \end{displaymath}$

(23)

estendendo-se a integral ao longo de toda a curva fechada. Aqui 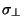$\sigma_{\perp}$ é a componente de 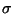$\sigma$ perpendicular a 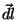$\vec{dl}$ . Seja 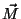$\vec{M}$ a magnetização do material. Vamos mostrar posteriormente que a corrente de magnetização de superfície é dada por 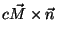$c \vec{M}\times\vec{n}$ . Por enquanto, aceitemos que

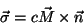$\begin{displaymath} \vec{\sigma}=c\vec{M}\times\vec{n} \end{displaymath}$

(24)

Então, qual será a corrente gerada por essa densidade superficial de corrente? Como 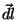$\vec{dl}$ é tangente à superfície, o vetor 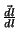$\frac{\vec{dl}}{dl}$ é um vetor unitário, tangente à superfície do condutor e também à curva

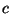. O vetor 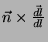$\vec{n}\times\frac{\vec{dl}}{dl}$ é tangente à superfície e perpendicular a 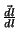$\frac{\vec{dl}}{dl}$ e é unitário. Logo, 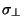$\sigma_{\perp}$ é dada por

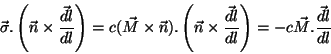$\begin{displaymath} \vec{\sigma}.\left(\vec{n}\times\frac{\vec{dl}}{dl}\right)= ... ...times\frac{\vec{dl}}{dl}\right)= -c\vec{M}.\frac{\vec{dl}}{dl} \end{displaymath}$

(25)

Então

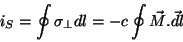$\begin{displaymath} i_S=\oint \sigma_{\perp}dl = -c\oint\vec{M}.\vec{dl} \end{displaymath}$

(26)

Next: Tratamento completo da magnetização Up: Magnetismo da matéria Previous: Interpretação de

Henrique Fleming 2002-12-24